Derivative of Fourth Root of x: Proof by First Principle

The derivative of fourth foot of x is equal to 1/(4x^3/4). Fourth root of x is denoted by ∜x = x^1/4, so its derivative formula is given by

$\dfrac{d}{dx}$(∜x) = $\dfrac{1}{4x^{3/4}}.$

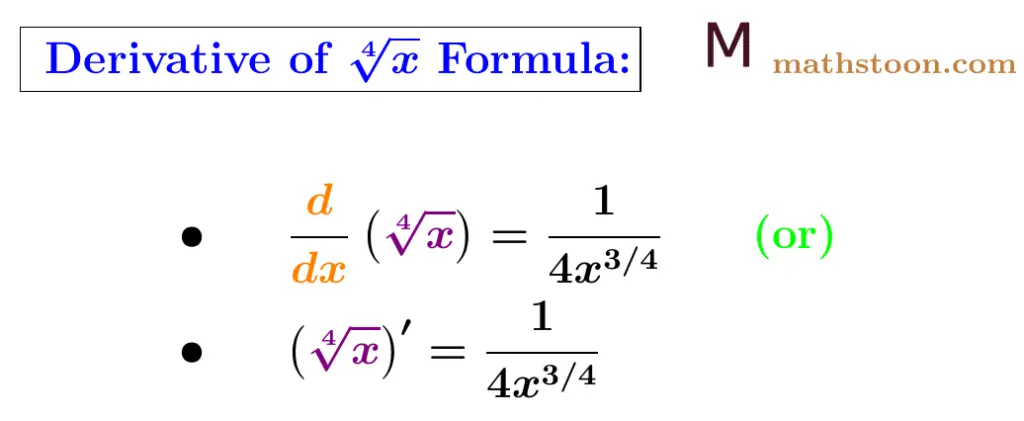
In this article, we will learn how to differentiate fourth root of x with respect to x by the following methods:

• Power rule of derivatives
• Substitution method
• First principle of differentiation
• Logarithmic differentiation.

By Power Rule

As the fourth root of x is expressed as ∜x = x^1/4, its derivative can be easily computed by the power rule of differentiation. This rule says that the derivative of xⁿ is equal to nx^n-1, that is,

d/dx (xⁿ) = nx^n-1.

Put n=1/4.

So we obtain that

$\dfrac{d}{dx}$(∜x) = $\dfrac{d}{dx}(x^{1/4})$ ⇒ $\dfrac{d}{dx}$(∜x) = $\dfrac{1}{4}x^{\frac{1}{4}-1}$ ⇒ $\dfrac{d}{dx}$(∜x) = $\dfrac{1}{4x^{3/4}}$.

So the derivative of fourth root of x by power rule is equal to 1/(4x^3/4).

ALTERNATIVE METHOD: To find the derivative of fourth root of x, let us substitute $y=\sqrt[4]{x}.$. This implies that

y⁴=x.

Differentiate both sides with respect to x. So we get that

$4y^3 \dfrac{dy}{dx}=1$

⇒ $\dfrac{dy}{dx}=\dfrac{1}{4y^3}$

⇒ $\dfrac{dy}{dx}=\dfrac{1}{4(\sqrt[4]{x})^3}$ as we have $[\because y=\sqrt[4]{x}]$

⇒ $\dfrac{dy}{dx}=\dfrac{1}{4x^{3/4}}$

This proves that the derivative of fourth root of x is 1/(4x^3/4), and we get this by the substitution method.

Also Read: Derivative of cube root of x

Derivative of Fourth Root of x by First Principle

By first principle, the derivative of f(x) is given by the following limit formula:

d/dx (f(x)) = lim_h→0 $\dfrac{f(x+h)-f(x)}{h}$.

Let f(x) = ∜x. Note that

f(x) = x^1/4 and f(x+h) = (x+h)^1/4.

Then by first principle,

$\dfrac{d}{dx}$(∜x) = limh→0 $\dfrac{(x+h)^{\frac{1}{4}} – x^{\frac{1}{4}}}{h}$

Put x+h = z. So z→x as h→0. Also, h=z-x.

Therefore,

So $\dfrac{d}{dx}$(∜x) = limz→x $\dfrac{z^{\frac{1}{4}} – x^{\frac{1}{4}}}{z-x}$ = $\dfrac{1}{4}x^{\frac{1}{4}-1}$. Here we have used the formula limx→a (xn-an)/(x-a) = nan-1.

Hence, $\dfrac{d}{dx}$(∜x) = $\dfrac{1}{4x^{3/4}}$.

Therefore, the derivative of fourth root of x is equal to 1/(4x^3/4) and this is obtained by the first principle of differentiation.

Related Topics:

Derivative of esinx	Derivative of log5x
Derivative of 1/x	Derivative of sin3x

By Logarithmic Differentiation

Let y = ∜x = x^1/4.

Taking natural logarithms on both sides, we get that

ln y = 1/4 ln x

Differentiating with respect to x,

$\dfrac{1}{y} \dfrac{dy}{dx}=\dfrac{1}{4} \cdot \dfrac{1}{x}$

⇒ $\dfrac{dy}{dx}=\dfrac{y}{4x} = \dfrac{x^{1/4}}{4x} = = \dfrac{1}{4x^{3/4}}$.

So by logarithmic differentiation, the derivative of fourth root of x is equal to 1/(4x^3/4).

Solved Problems

Question 1: Find the derivative of fourth root of a where a is a constant. That is, find d/dx(∜a).

Answer:

Note that the fourth root of $a$ is a constant. We know that the derivative of a constant is zero. So we obtain that

d/dx(∜a) = 0.

⇒ d/dx(a^1/4) = 0.

Remark: Put a=1. So the derivative of fourth root of 1 with respect to x is equal to 0, that is, d/dx(∜1) = 0.

Question 2: Find the derivative of fourth root of x+1, i.e, find d/dx(∜(x+1)).

Answer:

Put t=x+2.

So dt/dx = 1.

Now by the chain rule of derivatives,

$\dfrac{d}{dx}$ (∜(x+1)) = $\dfrac{d}{dt}$ (∜t) × $\dfrac{dt}{dx}$

= 1/(4t^3/4) × 1

= 1/{4(x+1)^3/4}.

So the derivative of (x+1)^1/4, that is, fourth root of x+1 is equal to 1/{4(x+1)^3/4}.

FAQs