Limit of sinx/x as x approaches infinity: Formula, Proof

The limit of sinx/x as x approaches infinity is denoted by lim_x→∞ (sinx/x) and its value is 0. So the limit formula of sinx/x as x→∞ is given as follows:

lim_x→∞ $\dfrac{\sin x}{x}$ = 0.

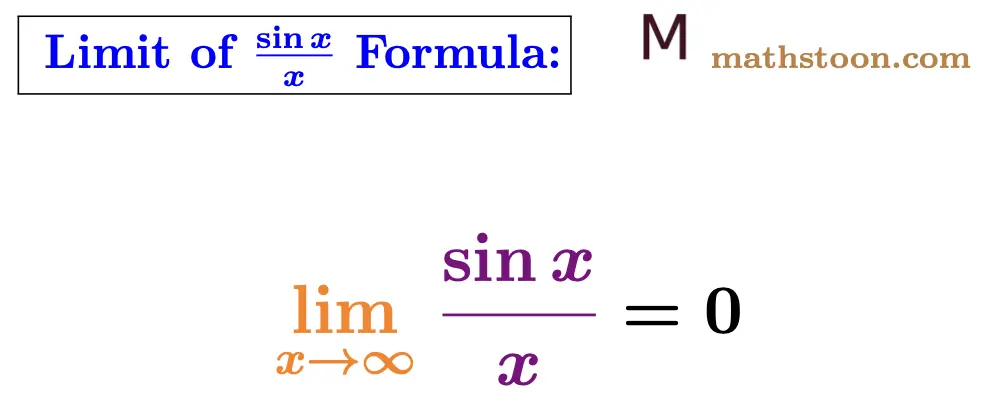
This limit formula can be proved using the Squeeze theorem of limits (also known as the Sandwich Theorem).

Evaluate lim_x→∞ (sinx/x)

Answer: The value of lim_x→∞ (sinx/x) is 0.

Explanation:

For all real values of x, we know that

-1 ≤ sin x ≤ 1.

So for large values x, we deduce that

$-\dfrac{1}{x} \leq \dfrac{\sin x}{x} \leq \dfrac{1}{x}$.

Now taking lim_x→∞, we deduce that

lim_x→∞ $\dfrac{-1}{x}$ ≤ lim_x→∞ $\dfrac{\sin x}{x}$ ≤ lim_x→∞ $\dfrac{1}{x}$

⇒ 0 ≤ lim_x→∞ $\dfrac{\sin x}{x}$ ≤ 0.

So by the Squeeze theorem, it follows that lim_x→∞ (sinx/x) = 0.

Therefore, the value of lim_x→∞ (sinx/x) is equal to 0, proved by the Squeeze/Sandwich theorem of limits.

Now, we will use this limit formula to find the limit of sinx/x² when x tends to infinity.

Limit of sinx/x² as x approaches infinity

Answer: The limit of sinx/x2 is 0 when x→∞, that is, limx→∞ (sinx/x2) = 0.

Method1:

lim_x→∞ (sinx/x²) = lim_x→∞ $(\dfrac{\sin x}{x} \times \dfrac{1}{x})$

⇒ lim_x→∞ (sinx/x²) = lim_x→∞ $\dfrac{\sin x}{x}$ × lim_x→∞ $\dfrac{1}{x}$ by the properties of limits.

⇒ lim_x→∞ (sinx/x²) = 0 × 0 = 0, by the above limit formula.

⇒ lim_x→∞ (sinx/x²) = 0.

So the limit of sinx/x² as x approaches infinity is equal to 0.

Method2:

As -1 ≤ sin x ≤ 1, for large values of x we obtain that

$-\dfrac{1}{x^2} \leq \dfrac{\sin x}{x^2} \leq \dfrac{1}{x^2}$.

Taking limit x tends to ∞, we deduce that

$0 \leq \lim\limits_{x \to \infty} \dfrac{\sin x}{x^2} \leq 0$.

So by Sandwich theorem, lim_x→∞ (sinx/x²) = 0.

Limit of sin2x/x as x approaches infinity

Put z=2x. So z→∞ as x→∞.

Then, $\lim\limits_{x \to \infty} \dfrac{\sin 2x}{x}$

= $\lim\limits_{z \to \infty} \dfrac{\sin z}{z/2}$

= 2 $\lim\limits_{z \to \infty} \dfrac{\sin z}{z}$

= 2 × 0 = 0, by the above limit formula.

Hence the limit of sin2x/x as x approaches infinity is equal to 0.

Related Topics:

• Proofs of all Limit Properties
• Proofs of all Limit formulas

Limit of x sin1/x as x approaches infinity

Question: Find the limit of $x \sin \frac{1}{x}$ as x→∞.

Answer:

Put z=1/x. So z→0 when x→∞.

Now, $\lim\limits_{x \to \infty} x \sin \frac{1}{x}$

= $\lim\limits_{x \to \infty} \dfrac{\sin \frac{1}{x}}{\frac{1}{x}}$

= $\lim\limits_{z \to 0} \dfrac{\sin z}{z}$

= 1, by the limit formula lim_x→0 (sinx/x) = 1.

So the limit of xsin(1/x) as x approaches infinity is equal to 1.

FAQs